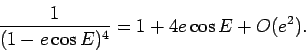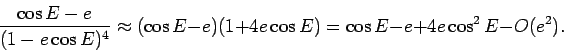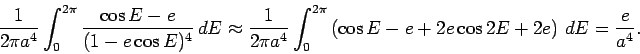Next: Interpretation of the result
Up: master
Previous: Perturbations in the pericenter
Now we compute the orbital average of perturbations, i.e., the
orbital average of  which will give its secular
perturbations. The derivative of the first component (
which will give its secular
perturbations. The derivative of the first component (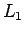 ), from
(29) is
), from
(29) is
The real work is to compute the orbital average
where  is mean anomaly. But since the semi-major axis of the ellipse was aligned with the x-axis, parts of
the integral with
is mean anomaly. But since the semi-major axis of the ellipse was aligned with the x-axis, parts of
the integral with 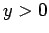 and
and  will cancel each other, yielding zero
for the integral. Therefore,
will cancel each other, yielding zero
for the integral. Therefore,
We have to do actual computation for 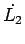 , i.e., we need
, i.e., we need
We change the variable of integration from  to
to  (eccentric
anomaly). Both change from
(eccentric
anomaly). Both change from 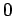 to
to  for a full orbit. We have
Kepler's equation
for a full orbit. We have
Kepler's equation
which gives
We also have
Then
This integral can be computed analytically. In
principle, we can compute 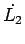 for any value of
for any value of  . This computation will be left as an exercise.
. This computation will be left as an exercise.
We, however, take the easy road and use an expansion in the
eccentricity  . The Taylor series gives us
. The Taylor series gives us
Therefore we have
From Trigonometry we recall that
and we get
Substituing this in the integral we get
With this, we have
where we (somewhat sloppily) replaced the  with
with  .
.
Subsections



Next: Interpretation of the result
Up: master
Previous: Perturbations in the pericenter
Werner Horn
2006-06-06
![]() which will give its secular
perturbations. The derivative of the first component (
which will give its secular
perturbations. The derivative of the first component (![]() ), from
(29) is
), from
(29) is

![]() , i.e., we need
, i.e., we need
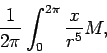
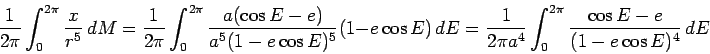
![]() . The Taylor series gives us
. The Taylor series gives us