


Next: Gravity fields and
Up: Secular precession of pericenter
Previous: Secular precession of pericenter
Let us collect now what we derived.
and
The derivative of  is in the ``
is in the ``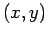 " plane, it is
perpendicular to
" plane, it is
perpendicular to  and it is a constant. Therefore,
and it is a constant. Therefore,  will
traverse a circle of radius
will
traverse a circle of radius 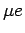 . The angular speed is the
velocity in the ``
. The angular speed is the
velocity in the `` " direction divided by the radius of the
circle. (If the speed is
" direction divided by the radius of the
circle. (If the speed is  and the radius is
and the radius is  , then the time
it takes to go around the circle is
, then the time
it takes to go around the circle is 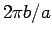 and the angular
speed is
and the angular
speed is  divided by how long it takes to traverse a full
circle, i.e.,
divided by how long it takes to traverse a full
circle, i.e.,
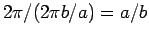 .)
.)
Hence, we have
Remember, this is an approximation, valid only for small
eccentricities. In particular, the longitude of pericenter,
 , measured from the
, measured from the  axis, has a secular perturbation
axis, has a secular perturbation
We can rewrite this, with the mean motion
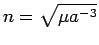 ,
as
,
as
In textbooks you will find similar expressions. What we derived is
the secular change for the longitude and not the
argument of pericenter. When you compare our results to those in
books, keep this in mind.
Geometrically speaking, we can think that the sattelite moves along an ellipse which rotates about its focus at an angular velocity of 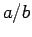 . This is of course only true for small eccentricities.
. This is of course only true for small eccentricities.
Exercise: Compute the secular part
of 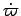 without expansions in eccentricity and compare
the result to those in textbooks. You will need the computation in
the next section in order to identify terms in the perturbations.
without expansions in eccentricity and compare
the result to those in textbooks. You will need the computation in
the next section in order to identify terms in the perturbations.



Next: Gravity fields and
Up: Secular precession of pericenter
Previous: Secular precession of pericenter
Werner Horn
2006-06-06
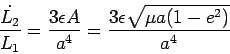
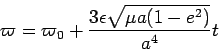
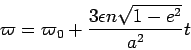
![]() . This is of course only true for small eccentricities.
. This is of course only true for small eccentricities.
![]() without expansions in eccentricity and compare
the result to those in textbooks. You will need the computation in
the next section in order to identify terms in the perturbations.
without expansions in eccentricity and compare
the result to those in textbooks. You will need the computation in
the next section in order to identify terms in the perturbations.