In this section we will investigate the two body problem in more
general terms. To do this consider the situation in the figure
below. There two bodies of masses ![]() and
and ![]() are at locations
are at locations
![]() and
and ![]() . We also assume that the only acting
force is the gravitational attraction between the two bodies:
. We also assume that the only acting
force is the gravitational attraction between the two bodies:

Newton's law implies
 |
(9) | ||
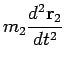 |
(10) |
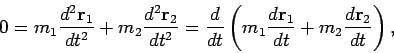
Conservation of Linear Momentum:
The center of mass of a two body system with no exterior forces moves at a uniform speed.
Since the motion of the center of mass is trivial we will ignore it for the remainder of this derivation. We will put the the origin of our reference frame at the center of mass.
To continue we multiply the equations motion by ![]() and
and ![]() respectively and
subtract the from each other to get
respectively and
subtract the from each other to get
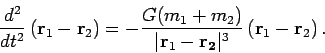
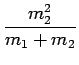 |
(11) | ||
 |
(12) |

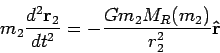
To continue we consider the motion of the mass ![]() :
:
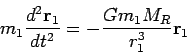
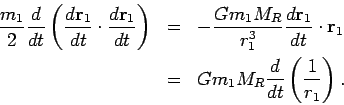
Conservation of Total Energy:
The total energy of the two body problem is constant.
For this last result, we computed the skalar product of the
equation of motion and the velocity. To continue we compute the
vector product of the equation of motion and ![]() . We will
have
. We will
have
![]() on the right and get:
on the right and get:
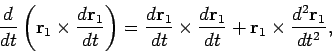
Conservation of Angular Momentum:
The Angular Momentum ![]() as defined in (15) is
constant.
as defined in (15) is
constant.
This is the third so-called conservation law. These laws are also called first integrals of the equation of motion.
The conservation of angular momentum has an important consequence.
Observe that the vector ![]() is perpendicular to the pair of
vectors
is perpendicular to the pair of
vectors ![]() and
and
![]() . Since
. Since ![]() is a constant vector, it is normal to a constant plane
containing
is a constant vector, it is normal to a constant plane
containing ![]() and
and ![]() , i.e. the two body problem
is a planar (two-dimensional) problem.
, i.e. the two body problem
is a planar (two-dimensional) problem.