Assumption: The center of mass of the two body system consisting is at rest or moves uniformly.
One can always arrive at this assumption by decomposing the motion
of the two body system into two pieces, a motion of the center of
mass and a motion of the two components with respect to the center
of mass. If we assume that there is no external forces (except the
gravitational forces between the two bodies), Newton's first law
tells us that the center of mass is either at rest or moves
uniformly. In the case of a satellite moving around Earth, this
assumption is not quite correct, since the center of mass moves in
the gravitational field of the sun, hence it is not a uniform
motion with constant speed. However, on the surface of the Earth the acceleration due to the
gravitational pull of the sun is approximately ![]() compared to Earth
gravity of
compared to Earth
gravity of ![]() , and we will ignore it for the time being.
, and we will ignore it for the time being.
We center our coordinate system at the center of gravity, which
sits on the line connecting the two bodies. In circular motion the
distance between the two bodies is constant ![]() . We have
. We have
![]() , where
, where ![]() is the distance of the body of mass
is the distance of the body of mass ![]() from the center of mass, and
from the center of mass, and ![]() is the distance of the body
of mass
is the distance of the body
of mass ![]() from the center of mass. We have from the
definition of the center of mass:
from the center of mass. We have from the
definition of the center of mass:
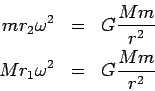
| (8) |
Examples: The ratio of the mass of the moon to the mass of
the earth is
Another more exciting example is from the search for extra solar
planets. Planets do not radiate any energy, and it is therefore
impossible to directly observe planets circling around stars.
However, if a large planet of mass ![]() circles a star of mass
circles a star of mass
![]() with period
with period ![]() we have the following:
we have the following:
