Economic Geography - Lab 4: Locational Indices

Gravity Models
The purpose of this exercise is to introduce students to measures of urban, retail or industrial gravity. The gravity models are roughly based on Newtonian physics, which states that big things have more gravity than small things and that gravitational pull is diminished by distance.
You'll use several formulas that use that logic. One is a standard gravity model, the other is called Reilly's Law of Retail Gravitation, a third formula allows you to use the first two to calculate a trade area for a location. The location could be a store, mall, city or county. All one needs are gravity factors (like populations or retail space(s)) and the distance between two or more locations.
The gravity model may help to determine the "pull" of a retail agglomeration like a city or a mall. Marketing geographers use it as part of a battery of decision-making tools. The I value that you'll calculate is a measure of interactive flows between two places and can be used to measure things like migration, or money or traffic flows
Here are some background readings:
- Partial Background Reading (find on Moodle)
- Wikipedia Short on Reilly's Law (note the links to a variety of other gravity models that can be used for other purposes)
- A Lesson on Reilly's Law from Syracuse University
- A Wisconsin University Web Site regarding Trade Area Analysis
Spatial Interaction Model
The first formula you will consider is a model of interaction between two locations. It includes a couple of scaling factors, which one would use to account for the friction of distance between two places. Some interactions (phone calls) exhibit very little friction of distance, whereas walking or driving a car (especially as gas prices increase) have significantly more costs in terms of time and effort, so the scaling factor will be higher.
NOTE: The tables below contain formulas. The formulas in the left column of each table are copied from a text. I have added other versions in the right column, that are equivalent, but perhaps students will find easier to translate in their minds.
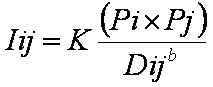 |
Iab=K(Pa*Pb)/(Dab)^s |
Where:
|
Where: Iab = Interaction between place A and place B |
Reilly's Law of Retail Gravitation
Another more common formula used by retail geographers is Reilly's law of retail gravitation. It also can help retailers and advertisers determine the trade area of their city or their particular business.
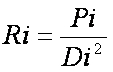 |
Ra=Pa/Dab |
Where:
|
Where: Ra= Retail gravitation of City A upon City B |
Frequently Reilly's formula is combined with other formulas to make it more useful. For example, you might want to calculate the number of trips people in a town (C) are likely to make to two competing neighboring towns (city A or city B). One such formula translates the R-values, derived from the above formula to simple percentages that can be more easily understood. The translation formula is as follows:
 |
Pac=Ra/(Ra+Rb)*100 |
Where: Pi= Percentage of retail trips (or trade) expected at place i from City X Ri= Reilly value of place i Rj= Reilly value of place j |
Where: Pac= Percentage of retail trips (or trade) likely to be made to City A from City C
|
Breakpoint Distance
Another useful formula, used in conjunction with Reilly's formula helps economic geographers calculate the comparative trade areas of a city (or store) by predicting the maximum distance people will be likely to travel to shop in one place or or its competiting place. For example, you may want to find out if people in City B will travel to City A to the north, or City C to the south.
You just need to know how far these three place are from each other and the populations of Cities A and B.
You'll calculate the trade area of cities A and C, and then see whether city B falls within the trade area of one or the other.
The breakpoint formula is below:
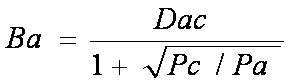 |
Bac = Dac/1+ (Square Root of (Pc/Pa)) |
Where:
|
Where: Bac= The trade area distance of city A as it extends toward City C |
If you add the breakpoint distances for both cities (Bac + Bca) it should equal Dac or Dca
City B may fall somewhere between City A and City C.
Scenario:
You have been hired to do some consulting work for a furniture store in Fresno. You have been asked to determine the geographic scope of an upcoming marketing campaign for the furniture retailer. Of course advertising will be concentrated in Fresno, but the dealer believes that her profit margin is dependent upon attracting customers from nearby counties. Still, a good campaign is expensive and the dealer does not want to waste money on marketing efforts in towns too distant to attract a significant number of customers. Many of the out-of-town customers will travel on California 99 from towns like Merced, Madera, Chowchilla, Hanford and Visalia. Those same customers may also chose to go to other cities, such as Modesto to buy furniture. So you want to attract them from a distance, but not waste money advertising in places where customers are too far away.
Your Task:
You are to determine the trade area for this furniture store. Use the formulas above to answer the questions below.
The data you need is in this Microsoft Excel table. It contains population information for 27 California Metropolitan Statistical Areas, plus latitude and longitude coordinates and a measure of distance between each of the cities in the table.
Download the formulas in Microsoft Excel if you get stuck. This file is probably used best to "check" your work. You could not use this file in a Geographic Information System.
Answers
You are to provide the following data to your boss by your next meeting. Don't use dollar signs or commas, just numbers or letters.
Here's a map to help you orient yourself.
View Retail Gravitation Maps in a larger map


