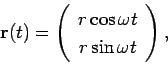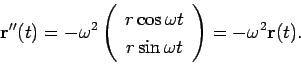Next: Example:
Up: Newton's Laws of motion
Previous: Kepler's laws
In this section we assume that the central body of mass  is
the earth and is fixed (or moving uniformly). And the second body
of mass
is
the earth and is fixed (or moving uniformly). And the second body
of mass 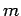 is a small artificial satellite. The Earth's mass
is a small artificial satellite. The Earth's mass
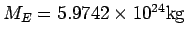 Sputnik I on the other hand
weighed 83.6 kg. So its gravitational pull on the Earth can
probably be neglected. (This is certainly not true for its effect
on world history or American politics).
We will also assume that the satellite moves on a circular orbit.
and that earth is at the center of this orbit.
Let
Sputnik I on the other hand
weighed 83.6 kg. So its gravitational pull on the Earth can
probably be neglected. (This is certainly not true for its effect
on world history or American politics).
We will also assume that the satellite moves on a circular orbit.
and that earth is at the center of this orbit.
Let  be the radius of the circular orbit. The distance
traveled after a time
be the radius of the circular orbit. The distance
traveled after a time  is given by
is given by
Hence,
The area swept in a time  is given by
is given by
Kepler's second law implies that this area is proportional to  .
It follows that
.
It follows that
for some constant angular velocity  . Thus we have the
rule:
. Thus we have the
rule:
Satellites on circular orbits must move at a constant angular
velocity.
In polar coordinates we have then
and therefore
(4) can thus be written as
or simply as
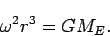 |
(6) |
If  is the period of this motion then
is the period of this motion then
substituting this into (6) we get
 |
(7) |
this is of course Kepler's third law in the special case of
circular orbits.
The expression  is called the geocentric gravitational
constant. Its value is
is called the geocentric gravitational
constant. Its value is
Subsections



Next: Example:
Up: Newton's Laws of motion
Previous: Kepler's laws
Werner Horn
2006-06-06