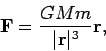Next: How does the above
Up: Newton's Laws of motion
Previous: Newton's Laws of motion
All of you have previously encountered Newton's laws of motion.
These laws form the basis of the part of mechanics which is known
as dynamics. They are as follows:
- A body does not change its state of rest or uniform
straight-line motion unless it is compelled by some force to
change that state.
- The change of motion is proportional to the force and takes
place in the same direction as the force.
- Action is always contrary and equal to reaction.
The first and second laws of motion are usually combined in a
single vector equation:
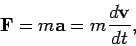 |
(1) |
where  is the force, the scalar
is the force, the scalar 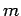 is the mass of the
body, and
is the mass of the
body, and 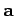 its acceleration. This simplified version
assumes tacitly that the mass is a constant. Often, in our daily
life experiences, this is a valid assumption or at least a good
approximation. But even, when you press the accelerator in a car
the mass of the car changes due to the burning of fuel and rubber.
However, this change is insignificant compared with the mass of
the vehicle and can be neglected.
its acceleration. This simplified version
assumes tacitly that the mass is a constant. Often, in our daily
life experiences, this is a valid assumption or at least a good
approximation. But even, when you press the accelerator in a car
the mass of the car changes due to the burning of fuel and rubber.
However, this change is insignificant compared with the mass of
the vehicle and can be neglected.
Accelerating rockets is always accompanied by huge changes of the
mass of the rocket itself. Furthermore, since space travel is
often done at very high velocities, relativity effects can play a
role, albeit a very minor one in the context of this class. To
account for this we use the following form of Newton's law:
 |
(2) |
where 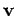 is the velocity of the body. It is easy to see
that (1.2) implies (1.1) for a constant mass.
is the velocity of the body. It is easy to see
that (1.2) implies (1.1) for a constant mass.
Newton also published his law of gravity
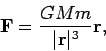 |
(3) |
where  is the attracting force between the two bodies of
mass
is the attracting force between the two bodies of
mass  and mass
and mass 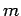 and
and 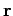 is a vector pointing from one
body to the other. The constant
is a vector pointing from one
body to the other. The constant 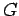 is the Gravitational constant
which is measured at
is the Gravitational constant
which is measured at
If the bigger of the two bodies were fixed at the origin of a coordinate system, and the mass 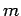 of
the smaller body were fixed, we could describe the motion of the
smaller body by
of
the smaller body were fixed, we could describe the motion of the
smaller body by
a coupled system of two first order ordinary differential
equations. Since 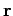 and
and 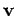 are vectors, it is
actually a coupled system of six ordinary differential equations.
Given initial conditions
are vectors, it is
actually a coupled system of six ordinary differential equations.
Given initial conditions 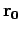 and
and 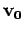 we can
describe all future positions of the body of mass
we can
describe all future positions of the body of mass 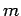 . This tells
us that we usually need seven variables to describe the motion
completely, time, three spatial components and three velocity
components.
. This tells
us that we usually need seven variables to describe the motion
completely, time, three spatial components and three velocity
components.
Subsections



Next: How does the above
Up: Newton's Laws of motion
Previous: Newton's Laws of motion
Werner Horn
2006-06-06