


Next: The Laplace vector
Up: Perturbations and more on
Previous: General formulae for perturbations
The energy for the Kepler motion is
Then,
or
After substituting the equations of motion for 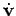 and
rearranging terms, we get
and
rearranging terms, we get
We need now
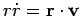 , and we get
, and we get
which simplifies to
This is what we expected, i.e. the change of the energy is proportional to the perturbation. In particular, since 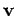 is tangential to the orbit, only the component of
is tangential to the orbit, only the component of
 tangential to the orbit changes the energy of the orbit.
Also note that when
tangential to the orbit changes the energy of the orbit.
Also note that when 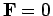 ,
,  is conserved.
Conserved quantities are often called first inetrals of the motion.
is conserved.
Conserved quantities are often called first inetrals of the motion.
Next, recall that the angular momentum
is defined as
and was also a conserved quantity (or first integral) of the unperturbed Kepler motion. To investigate the effect of the perturbation we
compute its time derivative
which after substituting 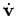 again yields
again yields
Here
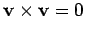 and
and
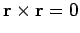 , leading to
, leading to
Note that only components of  which are perpendicular to
which are perpendicular to 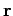 contribute to the change of the angular momentum. The quantity
contribute to the change of the angular momentum. The quantity
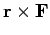 is known as the torque in mechanics.
is known as the torque in mechanics.



Next: The Laplace vector
Up: Perturbations and more on
Previous: General formulae for perturbations
Werner Horn
2006-06-06