


Next: Perturbation of the energy
Up: Perturbations and more on
Previous: Perturbations and more on
In the following we will use the same notations as before:
vectors are bold, time derivative is dot, 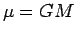 .
Position vector is
.
Position vector is 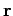 , velocity vector is
, velocity vector is 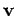 , i.e.,
, i.e.,
scalar product is
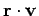 for two vectors,
for two vectors, 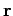 and
and
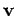 . The length of
. The length of 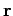 is
is 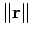 , also denoted by
, also denoted by  ,
the length of
,
the length of 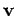 is
is
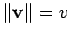 . We will need some basic facts from vector analysis.
. We will need some basic facts from vector analysis.
From
and
we obtain
The following general vector identity will be particularly useful::
Consider the perturbed Kepler problem
This is the differential equation for the Kepler problem which we encountered (and solved) before, however, it contains an addtional term
 which is the perturbation. For now we leave its form unspecified, but we note that we will assume that this force is small, when compared to the central gravitational force
which is the perturbation. For now we leave its form unspecified, but we note that we will assume that this force is small, when compared to the central gravitational force
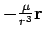 . The mass of
the particle whose motion is under consideration does not enter
our equations.
. The mass of
the particle whose motion is under consideration does not enter
our equations.



Next: Perturbation of the energy
Up: Perturbations and more on
Previous: Perturbations and more on
Werner Horn
2006-06-06
![]() .
Position vector is
.
Position vector is ![]() , velocity vector is
, velocity vector is ![]() , i.e.,
, i.e.,