This chapter will begin with a short history about Euclid and Greek mathematics. We will then dig into the mathematics, presenting the ideas the way Euclid did, using modern language as in John Casey's treatment in Euclid's Books 1-6 (www.gutenberg.org). We will present basic definitions of geometric objects, since this is a Common Core State Standard (G.CO.1: Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment, based on the undefined notions of point, line, distance along a line, and distance around a circular arc.). We will include GeoGebra applets like the one that follows to illustrate, in an interactive way, Euclid's postulates 1-4. Readers will then experiment with the following applet and thus be able to visualize Euclid's 5th postulate, which is equivalent to the parallel postulate.

Move point A around. (Keep it on ray HI and above line CD.)
What do you notice? (Write down at least two observations.)
What do you wonder? (Write down at least two questions.)

Next we will discuss why Euclid's 5th postulate is logically equivalent to the alternate interior angles theorem. In order to do this, we will first need to review the logical relationships and equivalencies of a statement, its converse, its contrapositive and its inverse ... (A review section of truth tables with examples and exercises will be included in an appendix.) This will serve to remind readers of various proof strategies (sometimes it's easier to prove the contrapositive of a statement, rather than the statement itself), which is a fundamental concern throughout the Common Core. We will refer interested readers to additional examples (not related to geometry) in an appendix.

We will reword the alternate interior angles proposition and the 5th postulate as in (http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI27.html):

Alternate interior angles Proposition (alternate interior angles)
If a straight line falls on two straight lines, then if the alternate angles are equal, then the straight lines do not meet.

Postulate 5
If a straight line falls on two straight lines, then if the alternate angles are not equal, then the straight lines meet [on a certain side of the line].

The above and below will emphasize reasoning stressed in the Common Core. For example, the geometry congruence standards include: PROVE GEOMETRIC THEOREMS ([Focus on validity of underlying reasoning while using variety of ways of writing proofs.])

Starting from the basic definitions and postulates, we will prove various theorems about lines and angles, focusing on theorems included in the Common Core. For example, the 9th Geometry Congruence Standard (G.CO.9) is: Prove theorems about lines and angles. Theorems include: vertical angles are congruent; when a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent; points on a perpendicular bisector of a line segment are exactly those equidistant from the segment’s endpoints. We will prove some theorems about triangles and homework will include other proofs from G.CO.10: Prove theorems about triangles. Theorems include: measures of interior angles of a triangle sum to 180°; base angles of isosceles triangles are congruent; the segment joining midpoints of two sides of a triangle is parallel to the third side and half the length; the medians of a triangle meet at a point. Some of the proofs about triangles may appear in Chapter 2, which is about transformation geometry, since transformation geometry plays a much larger role in the Common Core than most teachers are accustomed to. For example, both congruence and similarity of figures are to be understood in terms of rigid motions of the plane.

The following GeoGebra applet will allow the reader to discover properties of vertical angles.

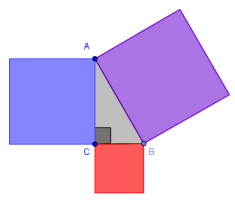
We will then show (as S. Brodie did or using ideas from cut-the-knot) that the parallel postulate is equivalent to the Pythagorean theorem.

Readers will learn the relationship between a circle's central and inscribed angles by experimenting with the following applet and answering the questions that follow.

Name a central angle using its vertex point and points on its sides; name an inscribed angle.
Write down at least two things you noticed when you moved point D around.
Write down at least two things you wonder about this experiment.
Make a conjecture about the relationship between an inscribed angle and its central angle.

Readers will be guided to prove the conjecture on their own and a detailed, visual proof will be included here (for those who use this material for self-study).

return to main page