


Next: First integrals and osculating
Up: Perturbations and more on
Previous: The Laplace vector
In order to compute the length of  , we need to prove the following formula
for the energy.
, we need to prove the following formula
for the energy.
where  is the semi-major axis. In particular, this provides a
simple way to compute semi-major axis. We use polar coordinates
is the semi-major axis. In particular, this provides a
simple way to compute semi-major axis. We use polar coordinates
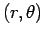 in the plane of the orbit. As before we have
that
in the plane of the orbit. As before we have
that
Now, consider the coordinate transformation
It follows that
which can be written as
This is the formula for rotation by the angle 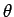 , which
preserves the length of vectors. Hence, the length of the left hand side
, which
preserves the length of vectors. Hence, the length of the left hand side 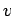 is the same as the length on the right, i.e.
is the same as the length on the right, i.e.
We return now to dealing with energy. We learned that the absolute value of the angular momentum
momentum 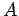 can be expressed as
can be expressed as
and that
where  is the parameter of the ellipse. We also have
is the parameter of the ellipse. We also have
From these, we get
Now we compute the energy in polar coordinates. Since the energy
is a constant, we compute its value at any time. We choose the
time of pericenter passage for convenience. Then  ,
which can be proved by differentiating the polar equation for the
orbit, and we also have from the same equation (with
,
which can be proved by differentiating the polar equation for the
orbit, and we also have from the same equation (with 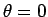 )
)
It follows that
and
Hence
and the desired formula for the energy is shown.
Now we return to the computation of the length of  .
From the energy relationship above, we have that
.
From the energy relationship above, we have that
and we also know that at pericenter passage
Hence
Finally,
Therefore, the length of  is
is 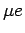 .
.
Notice that this result can be useful when computing orbital
elements.  provides both the direction of pericenter and the
eccentricity.
provides both the direction of pericenter and the
eccentricity.



Next: First integrals and osculating
Up: Perturbations and more on
Previous: The Laplace vector
Werner Horn
2006-06-06
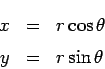
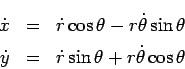
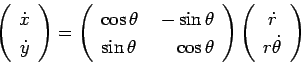
![]() can be expressed as
can be expressed as
![]() ,
which can be proved by differentiating the polar equation for the
orbit, and we also have from the same equation (with
,
which can be proved by differentiating the polar equation for the
orbit, and we also have from the same equation (with ![]() )
)
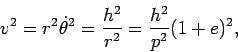
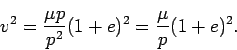
![\begin{displaymath}
\frac{1}{2}v^2 - \frac{\mu}{r} =
\frac{\mu}{2p}(1+e)^2 - ...
... - 2(1+e)\right] =
\frac{\mu}{2p}(e^2-1) = -\frac{\mu}{2a},
\end{displaymath}](img327.png)
![]() .
From the energy relationship above, we have that
.
From the energy relationship above, we have that
![]() provides both the direction of pericenter and the
eccentricity.
provides both the direction of pericenter and the
eccentricity.