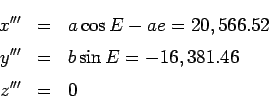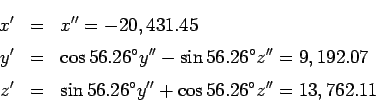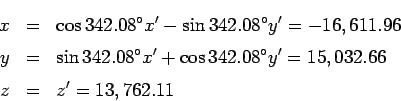In this section we will compute the cartesian coordinates of the satellite given as an example in a previous section. The two-line element was given by:
1 20361U 89097A 01154.90156813 -.0000008400000-0 00000-0 0 7462 2 20361 56.2556 342.0793 0127851 179.5306 322.3780 2.00562298 74668
We already calculated ![]() km. Furthermore, we have
km. Furthermore, we have ![]() . From this we get
. From this we get ![]() km. The next step is to compute the ecc3entric anomaly from Kepler's equation. The mean anomaly was given by
km. The next step is to compute the ecc3entric anomaly from Kepler's equation. The mean anomaly was given by
![]() . The numerical solution of Kepler's equation requires that we measure all angles in radians (You cannot do Calculus type operations with degrees ever!!). Transforming it into radians gives us
. The numerical solution of Kepler's equation requires that we measure all angles in radians (You cannot do Calculus type operations with degrees ever!!). Transforming it into radians gives us ![]() . We next perform the fixed point iteration with
. We next perform the fixed point iteration with
![]() . This gives us
. This gives us ![]() ,
, ![]() ,
,
![]() , and
, and ![]() . Since
. Since ![]() both are approximations to the eccentric anomaly with 5 valid digits. We will use
both are approximations to the eccentric anomaly with 5 valid digits. We will use ![]() . Using this we can directly compute the
. Using this we can directly compute the
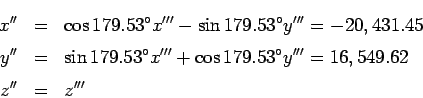
![]() coordinates of the satellite.
coordinates of the satellite.