


Next: Numerical Solution of Kepler's
Up: Kepler's Equation
Previous: The three anomalies
Kepler's equation connects the mean and the eccentric anomalies and is given by
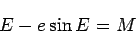 |
(23) |
To derive this equation, recall that the elliptic orbit is given by the
formula
Differentiating this with respect to time we get:
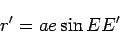 |
(24) |
On the other hand we have that
and hence
Differentiating this term we get
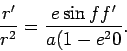 |
(25) |
Because of the equal area law we have
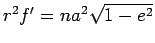 , where
, where  denotes the mean angular velocity
denotes the mean angular velocity 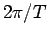 .
Using this we get from the last equation (25)
.
Using this we get from the last equation (25)
Comparing this with (24), we get
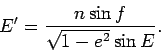 |
(26) |
However, from the last section we know that
and therefore
since 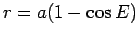 , this becomes
, this becomes
Integration over time yields
However, since 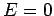 at
at 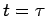 , the constant of integration
, the constant of integration 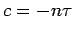 and
and
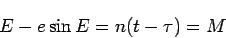 |
(27) |
which is Kepler's equation.
Kepler's equation makes it easy to compute the mean anomaly, whenever the eccentric anomaly is given, however, the other way round is difficult. The equation is a transcendental equation and astronomers have devised many numerical and analytic schemes to solve this equation. When the eccentricity  is very small,
the left hand side of (27) can be reasonably well approximated by
is very small,
the left hand side of (27) can be reasonably well approximated by
 itself, and therefore
itself, and therefore 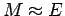 . In the next section we investigate a few methods that will give numerical solutions of Kepler's equation.
. In the next section we investigate a few methods that will give numerical solutions of Kepler's equation.



Next: Numerical Solution of Kepler's
Up: Kepler's Equation
Previous: The three anomalies
Werner Horn
2006-06-06
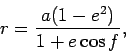
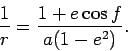

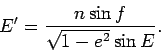
![]() is very small,
the left hand side of (27) can be reasonably well approximated by
is very small,
the left hand side of (27) can be reasonably well approximated by
![]() itself, and therefore
itself, and therefore ![]() . In the next section we investigate a few methods that will give numerical solutions of Kepler's equation.
. In the next section we investigate a few methods that will give numerical solutions of Kepler's equation.