We discussed solving first-degree equations in one variable in Mod. X. We now consider first-degree equations in two variables. A solution to an equation in two variables consists of a pair of numbers. A value for each variable is needed in order for the equation to be identified as true or false. It is customary to express the pairs of numbers as an ordered pair.

Consider the equation y = 3x - 4. If x = 1, then y = 3 (1) - 4 = -1. So, if x is replaced by 1 and y is replaced by -1, the equation is satisfied. We can also verify that each of the pairs of numbers given below also satisfy the equation.

If x = 0, y = -4. Ordered pair (0, -4)

If x = 3, y = 5 Ordered pair (3, 5)

If x = -2, y = -10. Ordered pair (-2, -10)

We usually write the pair in alphabetical order and use parentheses to express the fact that a specific order is intended. Hence (x, y) is the notation used to express ordered pairs for the equation y = 3x - 4. The specifice ordered pairs from the values above which satisfy the equation are (1, -1), (0, -4), (3, 5), and (-2, -10). In fact there are infinitely many ordered pairs which satisfy the given equation as well as all other first-degree equations in two variables. Each ordered pair found above is a solution of the equation y = 3x - 4.

Since there are infinitely many elements in the solution set, we must employ a way to display it other than listing the numbers of the set. Back in the 17th century, the French mathematician/philosopher Rene Descartes developed a method to display infinite sets of this type. He created what is now referred to as the rectangular, or Cartesian, coordinate system. It associates each ordered pair of real numbers with a unique point in the plane.

The graph of a linear equation is a line. We may graph a line if we know either two points on it or a point and the slope of the line. Let us begin this lesson by learning

How to graph a line.

In order to come up with a linear equation, we will need the following 3 formulas for lines.

The Slope Formula

Given two points, (x₁, y₁), and (x₂, y₂) the formula for slope, m, is

We notice that the slope of a line can be a positive number, a negative number, zero or no slope (undefined) as shown below:

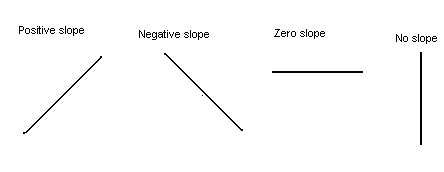
The Point-Slope Equation of a Line

We use the following equation when we are given a point and the slope:

Note, in the above, we plug in for x₁ and y₁, not x and y.

The Slope-Intercept Equation of a Line

We want to put all of our equations in this form, so that y is a variable in terms of x.

We also use this equation when we are given the y-intercept, (0, b), and the slope, m, of a line.
 

Let us try a few examples:

Example 1) Find the equation defined by the line that goes through the points (-3, 2) and (4, 16)

We begin by finding the slope between the two points. It does not matter which point you let be (x_1, y₁) and which one you let be (x₂ , y₂), as long as you are consistent when you plug into the formulas. Let us let (x_1, y₁) = (-3, 2) and (x₂ , y₂) = (4, 16), and plug into the formula for slope.

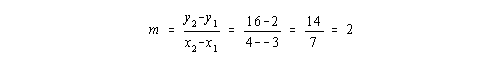
Now, we will use m= 2 and the point (-3, 2) and plug into the point-slope equation

We want to put all our lines in slope-intercept form, which means that we must solve for y.

Example 2) Find the function defined by the line with x-intercept 3 and y-intercept -5

Remember that an intercept is a point. So we may find the slope using the x-intercept, which is the point (3,0), and the y-intercept which is the point (0,-5).

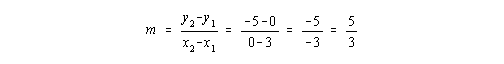
Since we now have the slope and the y-intercept, we may plug directly into the slope-intercept equation of a line. m = 5/3, and b = -5

Example 3) Find the function defined by the line through the two points (-7, 4) and (3, 4)

Again we begin by finding the slope. Let us let (x_1, y₁) = (-7, 4) and (x₂ , y₂) = (3, 4), and plug into the formula for slope.

So, m=0. Now plug into the point-slope equation of a line.

This is the equation of a horizontal line. Every horizontal line has slope 0.

Example 4) The boiling point of water is 100^o Celcius or 212^o Fahrenheit. The freezing point of water is 0^o Celcius or 32^o Fahrenheit. Find a formula for converting degrees of celcius to degrees of Fahrenheit.

Parallel Lines

Parallel lines have the same slope
 

Consider the following equation of a line: y = -2/3 x + 7. The line has slope -2/3, so any line parallel to it also has slope -2/3. We can use this fact to find the equations of line which are parallel.

Example 5) Find the equation of the line through (-2, 11) and parallel to the line 3x - 2y = 8.

We have a point but we need a slope. If we put the equation of the given line in slope-intercept form, we can find its slope, and since we want the equation of a line parallel, it will have the same slope.

So now we can see the slope is 3/2. Now we plug into the point-slope equation using m= 3/2 and the point (-2,11) and solve for y.

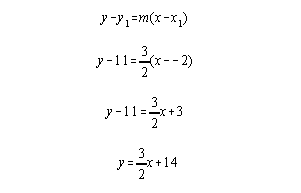
Perpendicular Lines

Perpendicular lines meet at a right angle. Their slopes are negative reciprocals of one another.
 

We can use the relationship of the slopes of perpendicular lines, to find the equations of perpendicular lines. Given the line y = 5x - 3, its slope is 5, so every line perpendicular to it has slope -1/5.

Example 6) Find the equation of a line through the point (1, -5) and perpendicular to the line -4x + 2y = -7.

First we put the line in slope-intercept form.

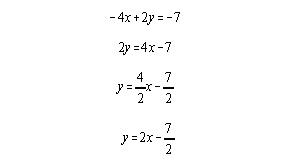
The above line has slope, m = 2. So a line perpendicular has slope m = -1/2. Now we plug into the point-slope equation using m = -1/2 and the point (1,-5)

Now you try a few:

Find the linear equation associated defined by each of the following lines.

1. going through points (-3,2) and (9, 26)

2. going through (5, -6) and with slope 2

3. y-intercept 4, and slope 1/3

4. A horizontal line through the point (-5, 3)

5. A line parallel to y = -3x + 2 and through the point (-8, 13)

6. A line perpendicular to y = -3x + 2 and through the point (-8, 13)

7. A store manager figures that she can sell 135 items at $50 each. If the store has a sale, for each $2 decrease in the price they can sell an additional 5 items. Find an equation for the number of itmes sold based on the sale price.

1. passing through points (-3,2) and (9, 26)

y - y₁ = m(x - x₁)

y - 2 = 2(x - -3)

y - 2 = 2x + 6

y = 2x + 8

Back to the Problem

2. going through (5, -6) and with slope 2

Back to the Problem

3. y-intercept 4, and slope 1/3

Back to the Problem

4. A horizontal line through the point (-5, 3)

Recall that every horizontal line has slope 0. So using m = 0, we get

Back to the Problem

5. A line parallel to y = -3x + 2 and through the point (-8, 13)

Since the lines are parallel, they will have the same slope. So we use m = -3.

Back to the Problem

6. A line perpendicular to y = -3x + 2 and through the point (-8, 13)

Since the lines are perpendicular, the slope will be the negative reciprocal. So we use m = 1/3.

Back to the Problem

7. A store manager figures that she can sell 135 items at $50 each. If the store has a sale, for each $2 decrease in the price they can sell an additional 5 items. Find an equation for the number of items sold based on the sale price.

Back to the Problem