One Dimensional Euler's Equations of Gas Dynamics

In this example we use a one-dimensional second order semi-discretecentral scheme to evolve the solution of Euler's equations of gas dynamics

where the pressure, p, is related to the conserved quantities through the equation of state

with . The solution is evolved over the interval , from to . The initial conditions are those of a Sod shock tube

and Dirichlet boundary conditions (i.e., the conserved quantities take on the values specified by the initial conditions at either boundary). Solution computed with 400 cells and cfl number 0.75.

The images below display, from top to bottom and left to right, the profiles of density, x-velocity, and pressure at . Click on the individual images to see an animation from to

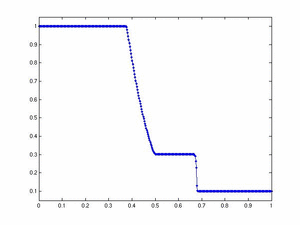
Click on the images above to see an animation