
Perimeter: The perimeter of a shape is the distance around that shape. This distance may consist of straight lines or curves. We can find the perimeter by adding the lengths of these lines and curves together. The first example we’ll consider consists of straight lines only.
Example 1) Find the perimeter of the following shape:

To find the perimeter of this shape we’ll
start in a corner and move clockwise around the shape adding the pieces
until we reach the starting point again. Notice that in this shape some
of the lengths are not given and have to be found.
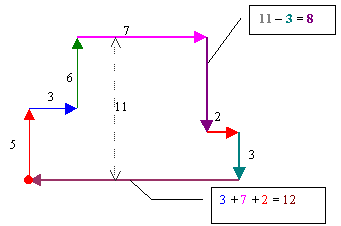 |
P= 5 +3 + 6 + 7 + 8 + 2 + 3 + 12 = 46 |
As mentioned earlier we may have portions
of circles as part of our shape. In order to find their lengths, we have
to use the formula for the distance around a circle or the circumference
of a circle.
|
|
Where "r" represents the length of the radius
of the circle and ![]() is a constant (approximately 3.14). In this course we will leave all answers
in their exact form (i.e. in terms of
is a constant (approximately 3.14). In this course we will leave all answers
in their exact form (i.e. in terms of ![]() ).
).
Example 2) Find the perimeter of the
following shape:

This shape consists of two line segments,
a quarter-circle, and a semi-circle. In addition to finding the length
of the arcs, we also have to find the length of the missing part in the
bottom segment.
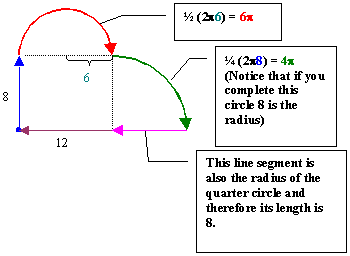
P= 8
+ 6![]() +4
+4![]() + 8 + 12
+ 8 + 12
P= 28 + 10![]()
Area:
The area of a shape is the number of 1 unit
by 1 unit squares (square units) that can fit inside of a shape. If our
shape is a rectangle or a square this number is easy to find. All we have
to do is multiply the length and the width of the shape. But if our shape
has slanted or curved parts, dividing it into smaller squares is not as
easily accomplished. To find the area of such shapes we have to rely on
formulas for the area of triangles and circles. The following table gives
you the formulas for the area of some basic shapes.
|
|
 |
|
|
|
 |
|
|
|
|
|
Now we can go back and find the area of the shape in example 2.
Example 3) Find the area of the
following shape:
| In order to find the area of this shape, we will divide it into three pieces; a rectangle (I), a semi-circle (II) and a quarter-circle (III). We will find the area of each piece separately and then find their sum. | 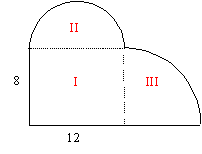 |
I : A = 12´ 8 = 96
II : A = ½ ![]() (62)
= ½ (36
(62)
= ½ (36![]() )
= 18
)
= 18![]() (We found ½ of the area of a full circle)
(We found ½ of the area of a full circle)
III: A= ¼ ![]() (82)
= ¼ (64
(82)
= ¼ (64![]() )
= 16
)
= 16![]() (We found ¼ of the area of a full circle)
(We found ¼ of the area of a full circle)
A= 96 + 18![]() + 16
+ 16![]()
A= 96 + 34![]()
Practice problems :
Find the Area and Perimeter for the following:
1. 
2. 
3. 
Solutions to sample Problems:
1.
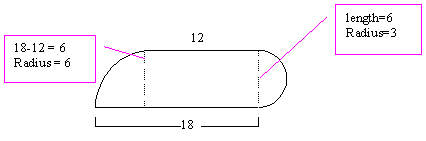
Perimeter= 18 + ![]() +12
+
+12
+![]() = 18+3
= 18+3![]() +12+3
+12+3![]() =
30+6
=
30+6![]()
Area= ![]() =
9
=
9![]() +72+4.5
+72+4.5![]() =
72+13.5
=
72+13.5![]()
2.

Perimeter= 10 +12 + ![]() =
22 + 5
=
22 + 5![]()
Area = 22 - ![]() = 22 – 12.5
= 22 – 12.5![]() (Notice that in this case we have to subtract the areas, but the perimeter
is still added. The perimeter is the distance around a shape and the fact
that this shape curves inward does not make the distance any shorter.)
(Notice that in this case we have to subtract the areas, but the perimeter
is still added. The perimeter is the distance around a shape and the fact
that this shape curves inward does not make the distance any shorter.)
3.

Perimeter= 24 +![]() +10+
+10+![]() =
24 + 7
=
24 + 7![]() + 10 + 7
+ 10 + 7![]() = 34 + 14
= 34 + 14![]()
Area = ![]() +
70 +
+
70 + ![]() = 12.25
= 12.25![]() + 70 + 12.25
+ 70 + 12.25![]() = 70 + 24.5
= 70 + 24.5![]()
Copyright © 1997 Bamdad Samii